पाइथागोरस थ्योरम क्या है | Pythagoras Theorem Kya Hai
पाइथागोरस प्रमेय (जिसे पाइथागोरस प्रमेय भी कहा जाता है) गणित का एक महत्वपूर्ण विषय है, जो एक समकोण त्रिभुज की भुजाओं के बीच संबंध की व्याख्या करता है। समकोण त्रिभुज की भुजाओं को पायथागॉरियन त्रिक भी कहा जाता है। इस प्रमेय के सूत्र और उपपत्ति को यहाँ उदाहरण सहित समझाया गया है।
पाइथागोरस प्रमेय मूल रूप से एक अज्ञात पक्ष की लंबाई और त्रिकोण के कोण को खोजने के लिए प्रयोग किया जाता है। इस प्रमेय से हम आधार, लंब और कर्ण के सूत्र प्राप्त कर सकते हैं। आइए यहां पाइथागोरस प्रमेय के गणित को विस्तार से जानें।
पाइथागोरस प्रमेय कहता है कि “एक समकोण त्रिभुज में, कर्ण भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है”। इस त्रिभुज की भुजाओं को लंब, आधार और कर्ण नाम दिया गया है। यहाँ, कर्ण सबसे लंबी भुजा है, क्योंकि यह कोण 90° के विपरीत है। समकोण त्रिभुज की भुजाएँ (कहते हैं a, b और c) जिनमें धनात्मक पूर्णांक मान होते हैं, जब वर्ग किया जाता है, तो उन्हें एक समीकरण में रखा जाता है, जिसे पायथागॉरियन ट्रिपल भी कहा जाता है।
पाइथागोरस प्रमेय की परिभाषा, पाइथागोरस प्रमेय क्या है | Pythagoras Pramey
गणित में पाइथागोरस प्रमेय बहुत ही सामान्य और महत्वपूर्ण विषय. यह समकोण त्रिभुज के विभिन्न पक्षों के बीच के संबंध की व्याख्या करता है. प्रमेय बताता है कि “एक समकोण त्रिभुज में, कर्ण का वर्ग त्रिभुज के अन्य दो पक्षों के वर्गों के योग के बराबर होता है.”
पाइथागोरस प्रमेय की परिभाषा इस प्रकार दी जा सकती है कि-
किसी समकोण त्रिभुज में कर्ण पर बना वर्ग (सबसे बड़ी भुजा पर बना वर्ग), आधार और लंब (शेष दो भुजाओं) पर बने वर्गों के योग के बराबर होता है।
पाइथागोरस प्रमेय का PROOF
समकोण त्रिभुज में, आधार और लम्ब एक-दूसरे के साथ 90 डिग्री का कोण बनाते हैं. इसलिए, पाइथागोरस प्रमेय के अनुसार, “कर्ण का वर्ग आधार के वर्ग और लंब के वर्ग के योग के बराबर है।”
“the square of the hypotenuse is equal to the sum of a base square and perpendicular square.”
इस प्रमेय को सिद्ध करने के लिए,
मान लें कि एक त्रिभुज ABC है, जिसका कोण B समकोण है।
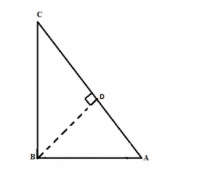
हमें सिद्ध करना है : AC²= AB² + BC²
To explain: हम एक सीधा रेखा BD खींचते हैं जो D पर AC से मिलती है।
Proof:
हम प्रमेय द्वारा जानते हैं कि यदि एक समकोण त्रिभुज के कर्ण से समकोण की ओर से खींचा जाता है, तो लम्बवत् के दोनों किनारों पर दो त्रिभुज एक दूसरे के समान होते हैं।
इसलिए,
△ADB ~ △ABC
Hence,
AD/AB = AB/AC (Condition for similarity)
Or, AB2 = AD × AC (1)
Also, △BDC ~△ABC (By applying the same theorem)
Therefore,
CD/BC = BC/AC (Condition for similarity)
Or,
BC2= CD × AC (2)
Now,
By adding the equations (1) and (2) we get,
AB2 + BC2 = AD × AC + CD × AC
AB2 + BC2 = AC (AD + CD)
Since, AD + CD = AC
Therefore, AC2 = AB2 + BC2
Hence, the Pythagorean theorem is proved.
पाइथागोरस थ्योरम | Pythagoras Theorem
पाइथागोरस प्रमेय की परिभाषा को ध्यान में रखते हुए इसके सूत्र को इस प्रकार लिखा जा सकता है। –
(कर्ण)² = (आधार)² + (लम्ब)²
माना कोई समकोण त्रिभुज है जिसके शीर्ष A, B और C हैं।

तो पाइथागोरस प्रमेय के अनुसार,
(AC)² = (BC)² + (AB)²
पाइथागोरस प्रमेय का उदाहरण | Example of Pythagoras Theorem in Hindi
उपरोक्त चित्र को देखिये। यदि उसमें आधार की लंबाई 5cm और ऊंचाई 12cm है तो कर्ण का क्या मान होगा?
हल – दिया है, आधार = 5cm, ऊंचाई, 12cm
ज्ञात करना है, कर्ण =?
पाइथागोरस प्रमेय के अनुसार,
(कर्ण)² = (आधार)² + (लम्ब)²
(AC)² = (BC)² + (AB)²
= 5² + 12²
= 25 + 144
= 169
AC² = 169
AC =√169
AC = 13 cm
अतः कर्ण का मान 13 cm होगा।
पाइथागोरस प्रमेय के अनुप्रयोग | Applications of Pythagoras Theorem
- यह जानने के लिए कि त्रिभुज समकोण त्रिभुज है या नहीं।
- एक समकोण त्रिभुज में, हम किसी भी भुजा की लंबाई की गणना कर सकते हैं यदि अन्य दो भुजाएँ दी गई हों।
- वर्ग का विकर्ण ज्ञात करना।
- यह जानने के लिए कि त्रिभुज एक समकोण त्रिभुज है या नहीं।
- एक वर्ग के विकर्ण को खोजने के लिए।
- समकोण त्रिभुज में, हम किसी भी पक्ष की लंबाई की गणना कर सकते हैं यदि हम अन्य दो पक्षों की लंबाई जानते हैं।
पाइथागोरस प्रमेय का चित्र | Images of Pythagoras


अधिक हिंदी विषय पढ़ने के लिए यहां क्लिक करें
FAQ | पाइथागोरस
Q1. पाइथागोरस प्रमेय का सूत्र क्या है
Ans – पाइथागोरस की प्रमेय अनुसार किसी भी समकोण त्रिभुज के कर्ण का वर्ग उसी समकोण त्रिभुज के लंब के वर्ग तथा आधार के वर्ग के योगफल के बराबर होता है।
अर्थात , (कर्ण)2 = (लंब)2 + (आधार)2
इस की सहायता से हम किसी समकोण त्रिभुज के कर्ण आधार व लंब का मान ज्ञात कर सकते हैं अगर हमें इन तीनों में से किन्हीं दो का मान भी दिया गया होता है तो तीसरे का मान हम इस सूत्र से आसानी से ज्ञात कर सकते हैं।
आधार, लम्ब तथा कर्ण में से सबसे बड़ी भुजा कर्ण होती है।
Q2. पाइथागोरस का जन्म कब हुआ
Ans – पाइथागोरस का जन्म 570 ईसा पूर्व में यूनानी द्वीप सामोस में हुआ था।
Q3. पाइथागोरस प्रमेय की खोज किसने की
Ans – पाइथागोरस प्रमेय की खोज ग्रीक के गणितज्ञ पाइथागोरस ने की थी। पाइथागोरस का जन्म इनके एक यूनानी दीप समूह में 570 ईसा पूर्व में हुआ था।
Q5. पाइथागोरस क्या है
Ans – पाइथागोरस की प्रमेय अनुसार किसी भी समकोण त्रिभुज के कर्ण का वर्ग उसी समकोण त्रिभुज के लंब के वर्ग तथा आधार के वर्ग के योगफल के बराबर होता है
पाइथागोरस प्रमेय को बोधायन प्रमेय भी कहा जाता है। इस की सहायता से हम किसी समकोण त्रिभुज के कर्ण आधार व लंब का मान ज्ञात कर सकते हैं अगर हमें इन तीनों में से किन्हीं दो का मान भी दिया गया होता है तो तीसरे का मान हम इस सूत्र से आसानी से ज्ञात कर सकते हैं।
क्या आप सरकारी या कंपनी की नौकरियों की तलाश कर रहे हैं, नवीनतम नौकरियों की जांच करें लिंक पर क्लिक करें। एचआर से संबंधित अद्यतनों पर नवीनतम लेख के बारे में जानने के लिए, यहां क्लिक करें। यदि आप बंगाल में विभिन्न विषयों पर प्रश्न उत्तर पढ़ने के इच्छुक हैं, तो यहां क्लिक करें। इसके अलावा, अगर आप स्वास्थ्य, सौंदर्य, वित्त, वित्तीय, व्यापार या ट्रेंडिंग टेक्नोलॉजी पर नवीनतम समाचार पढ़ने में रुचि रखते हैं, तो यहां क्लिक करें।




